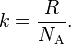What does formation energy mean?

I had read some theoretical paper about defect in GaN. They analysis the defect using formation energies as a function of Fermi level. If the formation energy is too big, this defect is very unlikely to be seen. So what does this “formation energy” mean?
The formation energy is the energy required to produce a defect (a vacancy) into the perfect crystal structure.In the case of GaN, the formation energy of each defect is a function of the Fermi energy and the difference of the chemical potentials between Ga and N.
The formation energy is the cost of creating a defect into an otherwise perfect solid. For a vacancy it is calculated as the energy needed to remove an atom from the bulk and take it to infinity. Formation energies are very important because the concentration of defects in a solid in thermodynamic equilibrium depends exponentially on it.

What's the differences among the concepts: binding energy, cohesive energy and formation energy?

• Formation energy is the change in energy when a material is formed from it's constituent elements in their reference states. For example, the formation energy of alumina (Al2O3) is the change in energy when fcc aluminum and O2 gas combine to make Al2O3.
• Cohesive energy is the amount of energy it takes to break something up into isolated atoms. This is also called the atomization energy.
• Binding energy in general means the amount of energy to split something up, and can mean different things depending on the context. For example, if you're talking about a molecule, it can refer to atomization energy.

Something to keep in mind regarding sign conventions is that formation energies are typically given as negative values, whereas cohesive energies and binding energies are typically positive values.

Standard enthalpy of formation

The standard enthalpy of formation or standard heat of formation of a compound is the change of enthalpy during the formation of 1 mole of the compound from its constituent elements, with all substances in their standard states at 1 atmosphere (1 atm or 101.3 kPa). Its symbol is ΔH_f^O or Δ_fH^O. The superscript theta (zero) on this symbol indicates that the process has occurred under standard conditions at the specified temperature (usually 25 degrees Celsius or 298.15 K). Standard states are as follows:

1. For a gas: the standard state is a pressure of exactly 1 atm
2. For a solute present in an ideal solution: a concentration of exactly one mole/liter (M) at a pressure of 1 atm
3. For a pure substance or a solvent in a condensed state (a liquid or a solid): the standard state is the pure liquid or solid under a pressure of 1 atm
4. For an element: the form in which the element is most stable under 1 atm of pressure. One exception is phosphorus, for which the most stable form at 1 atm is black phosphorus, but white phosphorus is chosen as the standard reference state for zero enthalpy of formation.^[1]

For example, the standard enthalpy of formation of carbon dioxide would be the enthalpy of the following reaction under the conditions above:

C_(s,graphite) + O_2(g) → CO_2(g)

All elements are written in their standard states, and one mole of product is formed. This is true for all enthalpies of formation.

The standard enthalpy of formation is measured in units of energy per amount of substance, usually stated in kilojoule per mole (kJ mol⁻¹), but also in calorie per mole, joule per mole or kilocalorie per gram (any combination of these units conforming to the energy per mass or amount guideline). In physics the energy per particle is often expressed inelectronvolts which corresponds to about 100 kJ mol⁻¹.

All elements in their standard states (oxygen gas, solid carbon in the form of graphite, etc.) have a standard enthalpy of formation of zero, as there is no change involved in their formation.

The formation reaction is a constant pressure and constant temperature process. Since the pressure of the standard formation reaction is fixed at 1 atm, the standard formation enthalpy or reaction heat is a function of temperature. For tabulation purposes, standard formation enthalpies are all given at a single temperature: 298 K, represented by the symbol ΔH_f298^O .

The standard enthalpy of formation is equivalent to the sum of many separate processes included in the Born-Haber cycle of synthesis reactions. For example, to calculate the standard enthalpy of formation of sodium chloride, we use the following reaction:

Na_(s) + (1/2)Cl_2(g) → NaCl_(s)

This process is made of many separate sub-processes, each with its own enthalpy. Therefore, we must take into account:

1. The standard enthalpy of atomization of solid sodium
2. The first ionization energy of gaseous sodium
3. The standard enthalpy of atomization of chlorine gas
4. The electron affinity of chlorine atoms
5. The lattice enthalpy of sodium chloride

The sum of all these values will give the standard enthalpy of formation of sodium chloride.

Additionally, applying Hess's Law shows that the sum of the individual reactions corresponding to the enthalpy change of formation for each substance in the reaction is equal to the enthalpy change of the overall reaction, regardless of the number of steps or intermediate reactions involved. This is because enthalpy is a state function. In the example above the standard enthalpy change of formation for sodium chloride is equal to the sum of the standard enthalpy change of formation for each of the steps involved in the process. This is especially useful for very long reactions with many intermediate steps and compounds.

Chemists may use standard enthalpies of formation for a reaction that is hypothetical. For instance carbon and hydrogen will not directly react to form methane, yet the standard enthalpy of formation for methane is determined to be −74.8 kJ mol⁻¹ from using other known standard enthalpies of reaction with Hess's law. That it is negative shows that the reaction, if it were to proceed, would be exothermic; that is, it is enthalpically more stable than hydrogen gas and carbon.

It is possible to predict heat of formations for simple unstrained organic compounds with the Heat of formation group additivity method.

(State: g = gaseous; l = liquid; s = solid; aq = aqueous)

Standard Enthalpies of Formation (at 25°C, 298 K)

Chemical Compound	Phase (matter)	Chemical formula	Δ Hf0 in kJ/mol
Acetone	l	C3H6O	−248.4
Acetylene	g	C2H2	+227.4
Ammonia	g	NH3	−46.1
Ammonia (Ammonium Hydroxide)	aq	NH3 (NH4OH)	−80.8
Ammonium nitrate	s	NH4NO3	−365.6
Benzene	l	C6H6	+49.1
Bromine	l	Br2	0
Bromine	g	Br2	+31
Bromine	g	Br	+111.9
Calcium	s	Ca	0
Calcium carbonate	s	CaCO3	−1207.6
Calcium oxide	s	CaO	−634.9
Carbon	s	C (graphite)	0
Carbon	s	C (diamond)	+1.88
Carbon dioxide	g	CO2	−393.5
Carbon monoxide	g	CO	−110.5
Chlorine	g	Cl2	0
Chlorine	g	Cl	+121.3
Copper(II) sulfate	aq	CuSO4	−769.98
Ethane	g	C2H6	−84.68
Ethanol	l	C2H5OH	−277.6
Ethylene	g	C2H4	+52.4
Fluorine	g	F2	0
Fluorine	g	F	+79.38
Glucose	s	C6H12O6	−1273.3
Hydrogen	g	H2	0
Hydrogen bromide	g	HBr	−36.3
Hydrogen chloride	g	HCl	−92.3
Hydrogen fluoride	g	HF	−273.3
Iodine	s	I2	0
Iodine	g	I2	+62
Isopropanol	g	C3H7OH	−318.1
Methane	g	CH4	−74.87
Methanol	l	CH3OH	−238.6
Nitric oxide	g	NO	+91.3
Nitrogen	g	N2	0
Nitrogen dioxide	g	NO2	+33.2
Oxygen	g	O2	0
Ozone	g	O3	+142.7
Propane	g	C3H8	−103.85
Silica	s	SiO2	−911
Silver	s	Ag	0
Silver chloride	s	AgCl	−127.0
Sodium	s	Na	0
Sodium	g	Na	+107.5
Sodium bicarbonate	s	NaHCO3	−950.8
Sodium carbonate	s	Na2CO3	−1131
Sodium chloride (table salt)	aq	NaCl	−407
Sodium chloride (table salt)	s	NaCl	−411.12
Sodium chloride (table salt)	l	NaCl	−385.92
Sodium chloride (table salt)	g	NaCl	−181.42
Sodium hydroxide	aq	NaOH	−470.1
Sodium hydroxide	s	NaOH	−426.7
Sodium nitrate	aq	NaNO3	−446.2
Sodium nitrate	s	NaNO3	−424.8
Sucrose	s	C12H22O11	−2226.1
Sulfur (monoclinic)	s	S8	0.3
Sulfur (rhombic)	s	S8	0
Sulfur dioxide	g	SO2	−296.8
Sulfur trioxide	g	SO3	−395.7
Sulfuric acid	l	H2SO4	−814
Water	l	H2O	−285.8
Water vapor	g	H2O	−241.82
Zinc sulfate	s	ZnSO4	−980.14

Boltzmann constant

Values of k	Units	Comments
1.38064852(79)×10−23	J/K	SI units, 2010 CODATA value, J/K = m2⋅kg/(s2⋅K) in SI base units[1]
8.6173324(78)×10−5	eV/K	2010 CODATA value[1] 1 electronvolt = 1.602176565(35)×10−19 J[1] 1/k = 11604.519(11) K/eV
2.0836618(19)×1010	Hz/K	2010 CODATA value[1] 1 Hz⋅h = 6.62606957(29)×10−34 J[1]
3.1668114(29)×10−6	EH/K	EH = 2R∞hc = 4.35974434(19)×10−18 J[1] = 6.579683920729(33) Hz⋅h[1]
1.0	Atomic units	by definition
1.38064852(79)×10−16	erg/K	CGS system, 1 erg = 1×10−7 J
3.2976230(30)×10−24	cal/K	1 steam table calorie = 4.1868 J
1.8320128(17)×10−24	cal/°R	1 degree Rankine = 5/9 K
5.6573016(51)×10−24	ft lb/°R	1 foot-pound force = 1.3558179483314004 J
0.69503476(63)	cm−1/K	2010 CODATA value[1] 1 cm−1 ⋅hc = 1.986445683(87)×10−23 J
0.0019872041(18)	kcal/(mol⋅K)	per mole form often used in statistical mechanics—using thermochemical calorie = 4.184 joule
0.0083144621(75)	kJ/(mol⋅K)	per mole form often used in statistical mechanics
4.10	pN⋅nm	kT in piconewton nanometer at 24 °C, used in biophysics
−228.5991678(40)	dBW/(K⋅Hz)	in decibel watts, used in telecommunications (see Johnson–Nyquist noise)
1.442 695 041...	Sh	in shannons (logarithm base 2), used in information entropy (exact value 1/ln(2))
1	nat	in nats (logarithm base e), used in information entropy (see Planck units, below)

The Boltzmann constant (k_B or k), named after Ludwig Boltzmann, is a physical constant relating energy at the individual particle level with temperature. It is the gas constant R divided by the Avogadro constant N_A:

The Boltzmann constant has the dimension energy divided by temperature, the same as entropy. The accepted value in SI units is1.38064852(79)×10⁻²³ J/K.

Since k is a physical constant of proportionality between temperature and energy, its numerical value depends on the choice of units for energy and temperature. The small numerical value of the Boltzmann constant in SI units means a change in temperature by 1 K only changes a particle's energy by a small amount. A change of 1 °C is defined to be the same as a change of 1 K. The characteristic energy kT is a term encountered in many physical relationships.